About
This website offers a modal logic model checker for Kripke models. These models can be build graphically using the provided interface on the main page. The model checker was developed for the Multi Agent Systems course at the Rijksuniversiteit Groningen for the academic year of 2017/2018.
Goal
The purpose of our application is to offer an intuitive tool to graphically create Kripke models. These models in turn allow inquiries to be made on them. Inspiration was drawn from homework assignments for the aforementioned course. These assignments required students to draw several Kripke models. When using pen and paper one is able to quickly draw a Kripke model, but is limited by its abilities to correct mistakes. Using digital software to create Kripke models is tedious, but does offer some flexibility. Our tool offers, in our view, the best of both worlds; fast iteration and flexibility. As such our tool aims to reduce human error when analyzing Kripke models.
Summary of the used logic
The system has the main purpose of deducing truth values of formulas based on epistemic logic. Epistemic logic is the logic considering knowledge: how do we reason about what we and others know? This logic turns out to be crucial in describing negotiating in the field of economics, parallel processes in the field of computer science and multi-agent systems in the field of Artificial Intelligence. Besides, epistemic logic is technically interesting: it has nice semantics.
Epistemic logic is an extension of classical propositional logic and therefore the provided system is also able to process pure propositional formulas except for quantifiers.
Kripke introduced a possible worlds semantics for this logic, in which a possible world is defined as an epistemic alternative for an agent in the logic.
A Kripke model contains these worlds, with relations between worlds with respect to the agent. You may view agents as humans, or as computer processors in a distributed system, or as other objects, according to the context.
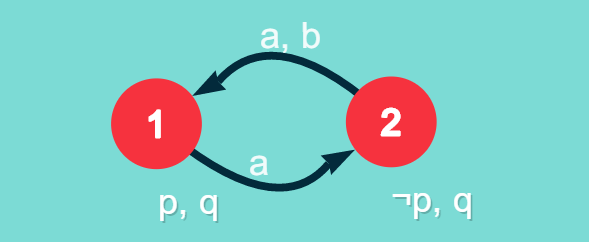
Formally A Kripke model M is a tuple (S,π, R1, ..., Rm) where: S is a non-empty set of states and π is a truth assignment to the propositional atoms per state. Figure 2 shows an example of a Kripke model. The R arrows indicate the relationships between states with corresponding truth values for atoms, and the number in the subscript indicates which agents has this relation. We generally evaluate a formula for 1 or more agents from a certain state given by (M,S) implies 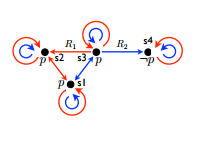
We now briefly explain the different systems of epistemic logic with associated operators.
System K(m)
This system uses all (instances of) tautologies from propositional logic with an operator Ki and Mi which works the same as the modal necessity and possibility operators.The K stands for knowledge, and the i for agent i. Kip stands for agent i knows p. MiP stands for agent i considers p to be possible. With respect to the Kripke model this means that in all worlds agent 1 considers possible, p is true and in at least one world agent 2 considers possible, p is true for respectively the K and M operator.
System S5(m)
System S5 consists of K plus a few axions. The added axioms are inter-related with the properties of the model. Axiom A3 states that everything that an agent knows is true. A4 defines that when an agent knows something, she also know this: positive introspection. A5 defines negative introspection. Both A4 and A5 draw a relation from a state to itself. A5* Looks like A4, if an agent considers something an epistemic alternative, she also knows that she holds this as an epistemic alternative.
Common knowledge
We now complete the system by adding the C and E operators. The operator E explains that every agent has the knowledge of a proposition from a given world. Hence, every agent knows the proposition within 1 alternative world away from the given world. The C operator on the other defines that everybody knows that everybody knows that everybody knows and so on. It is true for every agent from minimal 0 worlds away.
Implicit knowledge
The operator Ip states that it is implicitely known that p. This is true when p is true towards worlds with a union of relations, so all relations for all agents. Logical omniscience is an epistemological condition for implicit knowledge, but the agent may actually fail to realize this condition.
Implementation
Our model checker consists of two main parts. The first part offers a way to graphically construct a Kripke model and the second part a way to make inquiries upon said model.
Kripke Builder
The builder is separated into two files. One to specify the graph with all of its nodes and edges, the other actually implements all of the functionality of the builder. Each node is identified by a unique id (a positive integer value) and holds a specific label (representative of its id). The nodes id can be used to request the specific truth values of the atoms it holds. For example, looking at figure 1 we can request the truth value of atom p at node 1 and see that p holds. At node 2 however p does not hold. Currently the builder supports up to five different atoms { p, q, r, s, t }. This is a consciously set limit, for clarity, as our model checker is capable of a theoretical infinite amount of atoms.
Relations between nodes are determined by the edges. Edges contain information about from which node (id) it came and to which node it is flowing. It also hold information about the relation between nodes regarding agents. Only specified agents, represented as smaller case letters, are considered to have access to a certain node. In the case of figure 1 only agent a has access to node 2 from node 1, but both agent a and b can access node 1 from node 2. Again a limit is set on the number of agents ({ a, b, c, d, e }) that can be used for the same reasons as mentioned earlier.
Model Checker
The model checker performs several steps in order to analyses a certain query. At the first it does some preprocessing in order for the string-processing to right. Afterwards it operates based on two main files. The first of which simply offers helper methods for accessing the model and evaluation atoms, the second parses a given sentence and analyzes it recursively (a preview of which is given by the output tables in the examples). We slice a formula and decide what the main operator is. We then split left and right parts from the operator and have the same procedure from these sub-sentences until we have single atoms which we can evaluate from the model. We store parent-child pairs from sentences and sub-sentences from the sentence so we can later evaluate upwards. Whenever the parser observes an operator such as K,C,I,E,M or a negation (acting as a sort of formula), then we simply remove this operator and first parse on normally, while we store the operator connected to the sub-sentence. We then evaluate the formula bottom-up so we can actually evaluate truth values. We perform this last-mentioned for every world. This makes it possible for us to evaluate the sentence if we come across one of the function operators. We check the presence of functions in each layer before evaluating a higher layer.
Supported Formulas
As mentioned earlier, the supported formulas are Ki,C,I,E,Mi,!,T,F. Remember to always use correct parenthesis. So write KaKb(p) as Ka(Kb(p)). The supported operators are ^,v,> and =. Which convert to conjunction, disjunction, implication and bi-implications signs respectively.
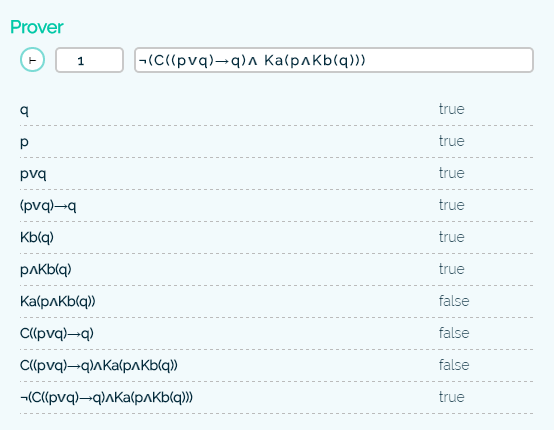
Examples
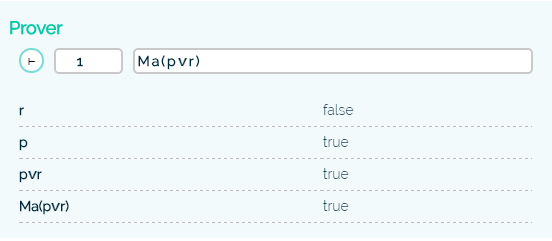
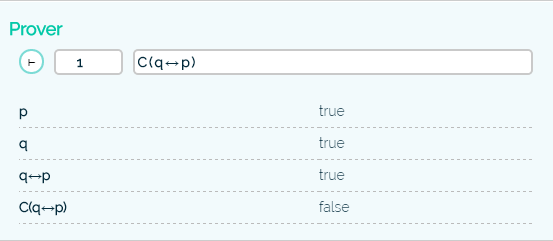
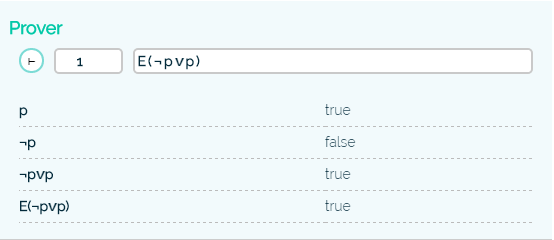
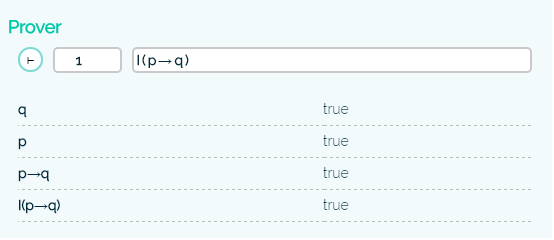
A few examples how the system breaks down a formula. Remember that you can specify the world on the left side of the formula. All the formulas are evaluated with respect to the model in figure 3.
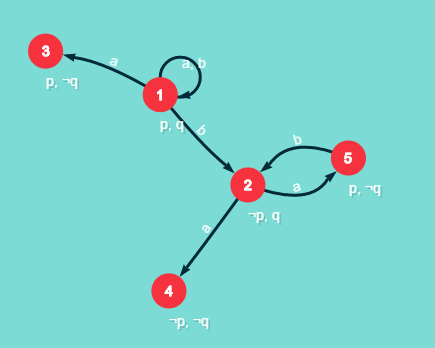
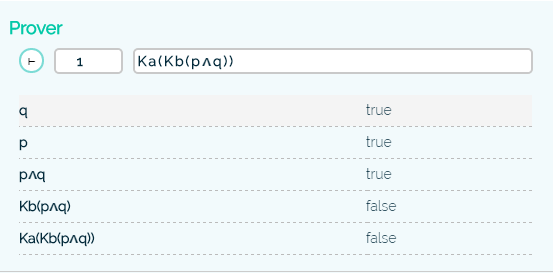
Improvements
Currently our tool requires you to write your sentences in full form. A future improvement might consist of converting user input automatically based on precedence rules. For example one might consider the following commonly used precedence of logical operators1:
| Operator | Precendence |
| ¬ | 1 |
| ∧ | 2 |
| ∨ | 3 |
| → | 4 |
| ↔ | 5 |
Another improvement is checking the cross browser compatibility. We did check for large discrepancies between different browser and everything apears to be fine. However differences between browsers can be subtle. Therefore ensuring cross browser compatibility can be time consuming. As this was largely irrelevant for the course and no major issues where found, no further development was done in this departement. As such we currently recommend using Chrome as your preferred browser when viewing this website. Further, the system does not check tautologies. Tautologies should be true irrespectively of the model. At the current state of the system the system could return false for tautologies in cases where it tries to retrieve the truth-value of non-existing propositions. An easy improvement would be to check for tautologies in the pre-processing step. However, it is not necessary to have this functionality because the system is more of a tool to check for truth-values with respect to an existing model for now. As last, we can improve by extending the current system to a system that supports beliefs.
References
1 O'Donnell, John; Hall, Cordelia; Page, Rex (2007), Discrete Mathematics Using a Computer, Springer, p. 120, ISBN 9781846285981.